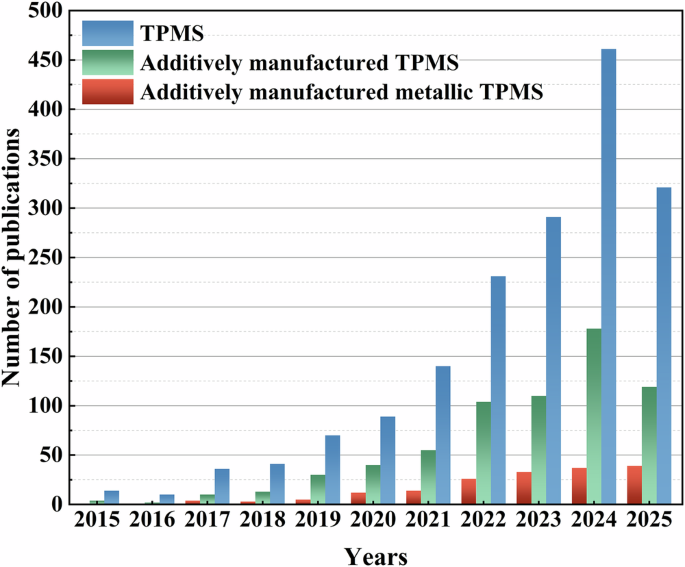
Model-based design of a mechanically intelligent shape-morphing structure

The modeling of smart materials holds significance in design processes. This study employs Finite Element Method (FEM) to describe the nonlinear characteristics of the pH-sensitive hydrogel and thermal response Shape Memory Polymer (SMP). pH-sensitive hydrogel and SMP are utilized as the smart materials integrated into the actuator. The pH-sensitive hydrogel is selected as the smart actuating material that can be used underwater due to their low cost, and high adaptability and sensitivity. In addition, the elevated pH levels in seawater, as opposed to air, create optimal conditions for activating pH-sensitive hydrogels. This property makes pH-sensitive hydrogels ideal materials for use in ocean engineering applications.Similarly, SMP is chosen based on the simplicity of achieving triggering conditions. The swelling and shrinking of the hydrogel induced to actuate the structure, while the shape memory effect of SMP applied as the stiffness enhanced method.

The pH-sensitive hydrogel modelling

Hydrogel exhibits hyperelastic properties and can be described by free energy theory to understand diffusion and deformation mechanisms³⁴. The free energy density of pH-sensitive hydrogels encompasses various contributing factors and expressed as,

where \(W\) is the free energy density, \(\mathbfF\) denotes the deformation gradient tensor, and \(C_H^+\), \(C_+\), \(C_-\) are nominal concentrations of hydrogen ions, mobile cations, anions, respectively. \(W_net\left(\mathbfF\right)\) is the elastic energy from polymer network stretching, that can be expressed by Neo-Hookean model as,

where \(N\) is the polymer chains number divided by the volume of the dry network, \(F_ik\) is the deformation gradient of the network, and the swelling volume is, \(\textdet\mathbfF=1+v_sC_s\), where \(C_s\) and \(v_s\) are the concentration of solvent and single molecule volume, respectively. Moreover, \(k\) is the Boltzmann constant and \(T\) is the absolute temperature. \(W_sol\left(\mathbfF\right)\) is from polymer–solvent mixing and described by Flory–Huggins model^35,36,

where \(\chi\) is the Flory–Huggins interaction coefficient, expressing the enthalpy of the mixing polymer. \(W_ion\left(\mathbfF,C_H^+, C_+, C_-\right)\) represents energy from ion–solvent, and mobile ions, with their low concentration, primarily affect free energy through mixing entropy,

and \(W_dis\left(\mathbfF,C_H^+, C_+, C_-\right)\) arises from acidic group dissociation in polymer chains,

where \(\gamma\) denotes the enthalpy increase, while \(C_A^-\) and \(C_AH\) represent fixed charge and associated acidic group concentration. The relationship between these concentrations requires, \(C_A^-=C_H^++C_+-C_-\) , and \(C_AH=f/v_s-(C_H^++C_+-C_-)\), in which \(f\) is the number of acidic groups on a polymer chain. The thermodynamic state of the system is entirely determined by the free energy, as described by Eq. (1). Once the explicit expression of the system’s free energy is obtained, the elastic stress of the hydrogel can be derived as,

where \(\mu _s\) represents the chemical potential. Using the osmotic pressure to express \(\mu _s\), the stress tensor can be expressed as,

The osmotic pressures from polymer–solvent and ion–solvent mixtures, denoted \(\Pi _sol\), and \(\Pi _ion\), respectively, are defined as,

where \(c_i\left(i=+,-,H^+\right)\) and \(\overlinec _i\left(i=+,-,H^+\right)\) describe the true concentrations of cations, anions and hydrogen ions inside and outside, respectively. In addition, the true concentrations and nominal concentrations are related as, \(C_i=c_i\textdet\mathbfF\). The \(\overlinec _H^+\) also relates to the pH of outside solution and is expressed as,

where \(N_A\) is the Avogadro number, \(N_A=6.023 \times 10^23\). In addition, the specific conditions are required for ionic equilibrium as³⁷,

By applying the Donnan equations and considering the principle of electroneutrality within the hydrogel, the following equation for acid dissociation is derived,

where \(K_a\) is constant of acidic dissociation. Equation (12) is expressed based on \(c_H^+\) that can be solved FEM solver. In the numerical simulation process, the Abaqus finite element solver is employed for the pH-sensitive hydrogel. A user-defined subroutine is utilized to describe the hyperelastic material based on the free energy function. It is assumed in this model that the volume per monomer is equivalent to the volume per solvent molecule. Additionally, the composition of the external solution is defined solely by \(\overlinec _+\) and \(\overlinec _H^+\). The electroneutrality in the outside solution needs to satisfy \(\overlinec _-=\overlinec _++\overlinec _H^+\), where \(\overlinec _H^+\) is considered as a variable calculated from the input pH value.

SMP modelling

The shape memory effect relating to the stiffness variation shows significant viscoelsticity, spanning temperatures both above and below the glass transition temperature^38,39. In our study, we employed the superimposed generalized Maxwell model and Williams-Landel-Ferry (WLF) equation within Abaqus finite element solver to elucidate the mechanical behavior of SMP. The utilized constitutive equations for the multi-branch viscos-elasticity are as follows⁴⁰,

where \(\sigma \left(t\right)\) represents stress at time t, \(\varepsilon _0\) is the strain at the initial time,\(E_n\) denotes the instantaneous modulus, \(E_i\) and \(\tau _i\) represent the elastic modulus and relaxation time of the Maxwell element i, respectively.

The relation of relaxation modulus E in the generalized Maxwell equation with time t is expressed as follows,

and satisfies the limit condition,\(\undersett\to \infty \textlimE\left(t\right)=E_n\). Conducting relaxation experiments at various temperatures and applying the time–temperature equivalence principle is essential. This allows the conversion of the relaxation response curve of SMP across different temperatures into a comprehensive relaxation response curve at a specific temperature. According to the WLF Eq. ⁴⁰, the connection between the relaxation time at the present temperature T and the relaxation time at the reference temperature of \(T_r\) can be written as,

where \(\alpha _T\) represents shift factor, \(C_1\) and \(C_2\) are material constant. And it is assumed that here the glass transition temperature (\(T_g)\) is same as \(T_r\).

Simulation setup

For the specific materials, poly(acrylic acid) (PAA) hydrogel, a widely recognized pH-sensitive hydrogel, is used as a reference in this study, with the polymer specified by several parameters. In particular, the representative value of volume of per water molecule is \(v_s=10^-28 m^3\), and the number of monomers per chain is \(1/Nv_s\). The chemical potential, normalized by \(kT\), is 4 × 10⁻²¹ J. For the PAA hydrogel, which exhibits a preference for large swelling ratios, the parameters \(Nv_s\) , f, and \(\chi\) are set to 0.001, 0.03, and 0.1, respectively. Additionally, the concentrations of anions \(\overlinec _-\) is 0.005 M and dissociation constant \(K_a\) is \(10^-4.3\), both of which are typical for carboxylic acids³⁷. The pH is set as the input parameter, which changes from 2 to 8. Furthermore, polylactic acid (PLA), recognized for its biodegradability, non-toxicity, and renewability, is selected as SMP for modeling⁴¹. The parameters related to the viscoelastic and thermal properties are set as, \(T_g=334 \textK\)\(C_1=6.14\) and \(C_2=293 \textK\)⁴². The material’s elastic modulus was 1000 MPa at 298 K, decreasing by 60% at the transition temperature⁴³. Consequently, the temperature range from 295 to 360 K was selected for the simulation.

For the remaining configurations, a standard 3D C3D8H mesh (8-node linear brick, hybrid with constant pressure) was selected to enhance mesh quality and convergence by addressing thin and irregular edges. Grid independence verification confirms global mesh sizes at around 0.5. Emphasis was exclusively placed on morphing structures in designing, with gravitational impact disregarded.