Optimal design of fractional-order proportional integral derivative controllers for structural vibration suppression

Each algorithm was run 30 times, with the number of iterations set to 100 under El Centro earthquake. The coefficients for all FOPID controllers, which were the average values derived from the 30 runs, are summarized for each optimization method in (Table 6). After being designed based on the El Centro earthquake, the controller design was evaluated using the other five earthquakes. This strategy tried to demonstrate the controllers’ effectiveness and practicality.

These controllers were optimized to provide the best results considering the five performance indices \(J_1\) to \(J_5\) introduced earlier. Table 7 presents the obtained values of the indices using the various algorithms under different earthquakes.

Considerable variations can be seen in the performance of the algorithms across different earthquakes in both examples. In the 3-story structure, for the El Centro earthquake, the CryStAl algorithm demonstrates its superiority with the lowest \(J_1\) value of 0.264, outperforming SPO (\(J_1=\) 0.326), PSO (\(J_1=\) 0.313), HS (\(J_1=\) 0.326), KH (\(J_1=\) 0.426), ACO (\(J_1=\) 0.452), GA (\(J_1=\) 0.303), GWO (\(J_1=\) 0.330), HHO (\(J_1=\) 0.296), SSA (\(J_1=\) 0.380), HO (\(J_1=\) 0.334), and DSA (\(J_1=\) 0.302). In terms of minimizing displacement, CryStAl performs approximately 23.7%, 15.7%, 23.4%, 61.8%, 71.7%, 43.2%, 10.5%, 10.4%, 30.5%, 21.0%, and 12.6% better than SPO, PSO, HS, KH, ACO, GA, GWO, HHO, SSA, HO, and DSA, respectively. For index \(J_2\), CryStAl (\(J_2\)= 0.285) once again demonstrates its efficiency, outperforming SPO (\(J_2\)= 0.326), PSO (\(J_2\)= 0.319), HS (\(J_2\)= 0.327), KH (\(J_2\)= 0.402), ACO (\(J_2\)= 0.435), GA (\(J_2\)=0.313), GWO (\(J_2\)=0.329), HHO (\(J_2\)=0.308), SSA (\(J_2\)=0.361), HO (\(J_2\)=0.331), and DSA (\(J_2\)=0.312). In terms of reducing acceleration, the performance of CryStAl is around 12.1, 10.4, 12.9, 29.2, 34.6, 8.95, 13.37, 7.47, 21.05, 16.1, and 9.5% better than SPO, PSO, HS, KH, ACO, GA, GWO, HHO, SSA, HO, and DSA, respectively.

Considering indices \(J_3\) and \(J_4\), CryStAl once again emerges as the top performer with \(J_3\)= 0.152 and \(J_4\)= 0.157, outperforming the other algorithms in minimizing both displacement and acceleration. On the other hand, in terms of index \(J_5\), CryStAl turns out to be the poorest algorithm, and though the differences between the algorithms are relatively small in terms of this index, CryStAl demonstrates a relatively high control force. The values of index \(J_5\) in the CryStAl algorithm for the 3-story building are respectively 24.78, 26.42, 24.94, 17.43, 20.45, and 25.16% higher than the average of that index of the other algorithms in the El Centro, Bam, Chi-Chi, Kobe, Northridge, and Turkey earthquakes, respectively. This indicates that the CryStAl algorithm yields greater force and superior results in all other indices for the 3-story building. The comparison in the 6-story example is more favorable for CryStAl. In some earthquake scenarios, such as Chi-Chi and Northridge, CryStAl even outperforms the average performance of other algorithms. This suggests that CryStAl requires lower forces to achieve the desired outcome compared to other algorithms.

In addition to comparing CryStAl with the other algorithms, it is important to note that the performance trends of different algorithms can vary across various indices. For instance, under the El Centro earthquake, the HHO algorithm achieves a higher score (0.296) in \(J_1\), while the GA algorithm performs slightly worse (0.303). However, examining the same case for the 6-story structure, we observe that the difference between these two algorithms under this criterion is greater. In terms of index \(J_2\), the SPO algorithm obtains almost the same score as the HS algorithm.

Similar to the 3-story building, in the case of the 6-story one, the CryStAl algorithm demonstrates its superiority over other algorithms in almost all the considered earthquakes. For instance, in terms of index \(J_1\), the CryStAl algorithm performs 37.44% better than the average of all algorithms under all examined earthquakes. However, it is crucial not to overlook the excellent performance of the GWO and DSA algorithms, which managed to achieve a similar level of performance as CryStAl in all earthquakes and outperform the other well-established algorithms. Furthermore, other algorithms such as HHO, SPO, and HO show commendable performance in most cases. As for the worst-performing algorithm, KH may be mentioned, which can be deemed the worst algorithm in half of the earthquakes in terms of index \(J_1\). However, in earthquakes like the one in Turkey, it performed better than algorithms such as GA, SSA, and SPO.

The DSA algorithm shows promise, particularly for the 3-story building. For the El Centro earthquake, DSA achieves indices between 0.302 (3-story) and 0.311 (6-story) for top-story displacement, often competing with the corresponding CryStAl values of 0.264 and 0.284. This trend continues across other earthquakes and other performance indices, suggesting DSA’s effectiveness, especially for smaller structures. Similar to DSA, HO demonstrates competitive performance across different earthquakes, turning out to be particularly effective for the 3-story building in some cases. For instance, for the El Centro earthquake, HO’s top-story displacement index ranges from 0.296 (3-story) to 0.491 (6-story), which is comparable to CryStAl’s results.

For further investigation, Fig. 5 shows the displacement responses of the structures during the aforementioned earthquakes. Figure 5a,b show the controlled responses achieved by the FOPID controller optimized using the CryStAl algorithm compared to those of the uncontrolled structure. The performance of the CryStAl algorithm in mitigating the seismic response through FOPID controller optimization has been evaluated. Figure 6a,b show displacement responses of the 3-story and 6-story structures under different earthquakes and CryStAl algorithms, respectively. Figure 5 provides additional evidence of the CryStAl algorithm’s effectiveness in significantly reducing structural response compared to other algorithms.

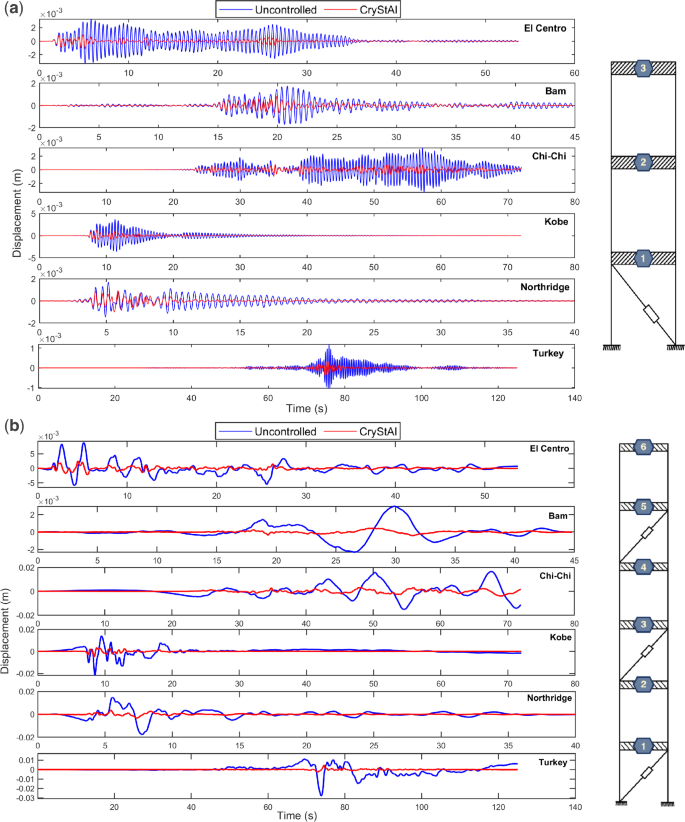
Displacement response of structures under different earthquakes with and without using the CryStAl algorithm. (a) The 3-story building. (b) The 6-story building.

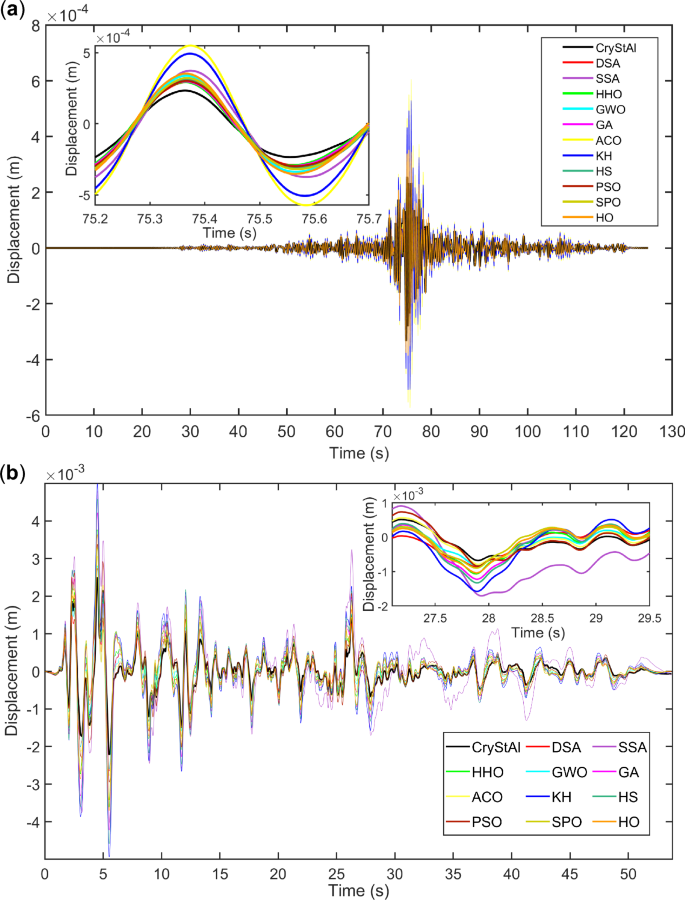
Comparison of the performances of various optimization algorithms. (a) Displacement response of the 3-story structure under the Turkey earthquake. (b) Displacement response of the 6-story structure under the El-Centro earthquake.

Figure 6 provides a comparison of the responses of various algorithms to showcase the differences between these algorithms, underscoring the high performance of the CryStAl algorithm in markedly diminishing structural vibrations. It is important to note that the results of other algorithms are qualitatively similar, making it difficult to discern the differences at this scale; to address this issue, a zoomed-in view of a part of the chart is provided in these figures to facilitate easier comparison between the algorithms. Figure 6a,b present the displacement responses of controlled structures under the Turkey and El-Centro earthquakes, respectively, using all the algorithms explored in this paper. In both cases, CryStAl demonstrated good performance in reducing seismic response.

Overall, the algorithms exhibited qualitatively similar behaviors in the two examples examined in this paper. However, the value of structural response reduction depends on various factors, including the properties of the structure, the earthquake load, and the controller. While structural properties and earthquake load characteristics remain constant during the optimization process iterations, the only factor that changes is the controller’s performance which is based on the inherent behavior of metaheuristic algorithms. Therefore, this process is repeated numerous times to obtain a relatively consistent pattern in controller behavior, allowing for a comparison of these controllers.

Table 8 presents a comparison of different algorithms used for earthquake analysis based on the reduction percentage and the absolute maximum displacement, velocity, and acceleration achieved. As can be seen from this table, during the El Centro earthquake, the Crystal algorithm demonstrated the most significant reduction, with percentages of 73.60 and 71.57%, corresponding to absolute maximum displacements of 0.88 and 2.50 mm, respectively, for the 3-story and 6-story structures. While ACO, PSO, HS, KH, SPO, GA, GWO, HHO, SSA, HO, and DSA achieved lower decrease percentages.

In the case of the 3-story building, in terms of displacement reduction during the El Centro earthquake, the algorithms closest in performance to CryStAl are the HHO and DSA, with reduction percentages of 70.44 and 69.77%, respectively. Similarly, in the case of the 6-story structure, the DSA algorithm exhibited the closest performance with a reduction percentage of 68.89%. Interestingly, the HHO algorithm even outperformed CryStAl in reducing the structural acceleration response by 2.12%. Comparable performance was also observed for this algorithm for the Bam, Kobe, and Northridge earthquakes. Under the Bam earthquake, HHO exhibited the closest performance to CryStAl in terms of displacement response reduction in the 3-story example. In terms of velocity and acceleration response reduction, the HHO algorithm had the second-highest reduction after CryStAl in the 3-story example. However, in the 6-story example, CryStAl ranked third. after PSO and DSA, in terms of velocity response reduction. Moreover, HHO again had the best performance in terms of acceleration response reduction in this example.

On average, the CryStAl, SPO, PSO, HS, KH, ACO, GA, GWO, HHO, SSA, HO, and DSA algorithms achieved displacement reductions of 65.48, 47.91, 61.98, 52.20, 61.21, 62.51, 60.80, 63.00%, 57.89, 60.15, and 62.67%, respectively, across all earthquakes in the case of the 3-story structure. For the 6-story structure, while this trend is qualitatively similar, the optimized controllers generally exhibited greater reductions in acceleration compared to the 3-story structure. In the 3-story example, the HHO algorithm achieved an acceleration response reduction 2.31% lower than that of CryStAl. From this comparison, it can be concluded that CryStAl performed better than HHO and the others in reducing displacement for the El Centro and almost all other earthquakes. In the Bam earthquake, CryStAl realized a decrease of 61.04% in the case of the 3-story structure for displacement response, while SPO, ACO, PSO, HS, KH, GA, GWO, HHO, SSA, HO, and DSA achieved lower decreases.

For the Chi-Chi earthquake, in the case of the 3-story structure, the CryStAl and HHO algorithms demonstrated displacement reductions of 71.40 and 70.93%, respectively. These algorithms achieved reductions of 76.23 and 68.87% in the case of the 6-story structure for the same earthquake. This comparison between the CryStAl and HHO algorithms illustrates their nearly similar behavior across different earthquake scenarios and various structures. In the case of the Kobe earthquake, for the 3-story example, the Crystal algorithm achieved a decrease of 72.47%, while the SPO algorithm (52.24%) turned out to be worse than HHO (70.01%), GWO (66.79%), SSA (62.21%), and DSA (69.36%). In the 6-story example, the DSA and GWO algorithms outperformed the HHO algorithm.

In the 3-story structure, the CryStAl algorithm achieved decreases of 42.30 and 72.10% for the Northridge and Turkey earthquakes, respectively. Overall, the CryStAl algorithm consistently achieves high decrease percentages and shows promising performance in reducing earthquake displacement. For the El Centro earthquake, the CryStAl, PSO, SPO, HS, KH, ACO, GA, GWO, HHO, SSA, HO, and DSA algorithms demonstrate significant reductions of 67.60, 54.52, 64.59, 63.86, 50.42, 63.936, 65.12, 63.71, 65.59, 61.06, 63.65, and 65.22% in the absolute maximum velocity, respectively; for the Bam earthquake, CryStAl again exhibits the highest reduction percentage of 56.90%, while SPO displays the lowest reduction percentage of 30.51%. The results of the remaining algorithms fall between these two extremes, with HHO at 50.02%, GA at 49.55%, PSO at 49.23%, HSM at 48.16%, GWO at 4568%, SSA at 43.01,% KH at 36.75%, HO at 44.38%, and DSA at 50.13%. In the case of the Chi-Chi earthquake, for the 3-story example, the reduction percentage varies between 60.50 and 76.49%, obtained by the SPO and CryStAl algorithms producing the highest and lowest values, respectively. Similarly, for the other earthquakes, the CryStAl algorithm achieved relatively high reduction percentages, indicating promising performance in mitigating earthquake-induced velocities.

The CryStAl algorithm consistently stands out by achieving significant decreases in acceleration across all earthquakes. It demonstrates an average reduction of 63.73 (3-story) and 70.98% (6-story), varying between 20.36 and 75.94% (3-story), and 30.10% and 80.47%(6-story), indicating its effectiveness for this seismic application. The HHO and DSA algorithms also deliver significant decreases in acceleration, demonstrating their potential for earthquake control.

Figure 7 illustrates the displacement and velocity of the third floor over time in both the uncontrolled and FOPID-controlled 3-story structures. This figure specifically displays the velocity responses of CryStAl under all the earthquakes. According to this plot, the controllers developed based on CryStAl are capable of effectively diminishing the displacement and velocity responses simultaneously.

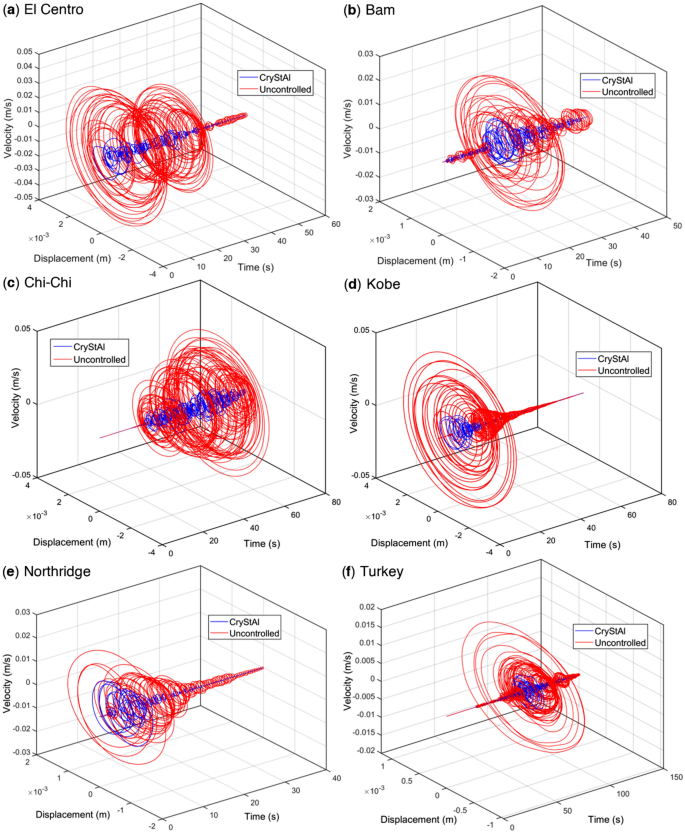
3D plots of the uncontrolled and FOPID-controlled 3-story structures under the various earthquakes.

Figures 8. 9 depict the displacement, velocity, and acceleration reductions achieved by all algorithms, demonstrating their effectiveness in controlling structural responses across the various earthquake scenarios.

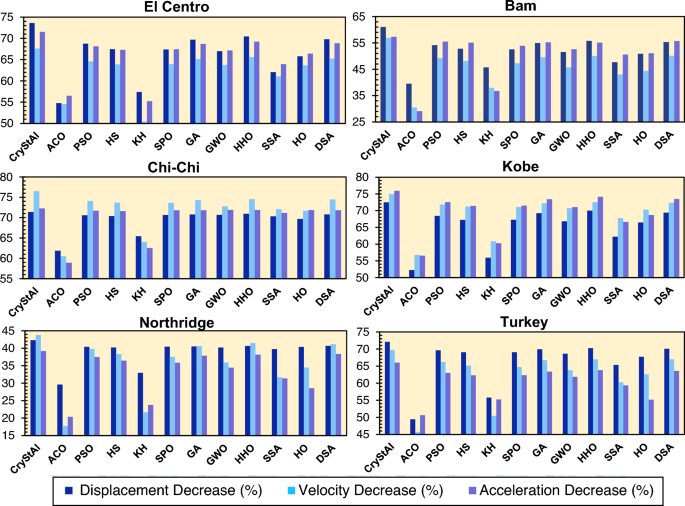
Performance of various algorithms in terms of displacement, velocity, and acceleration reductions for the 3-story structure under each earthquake scenario.

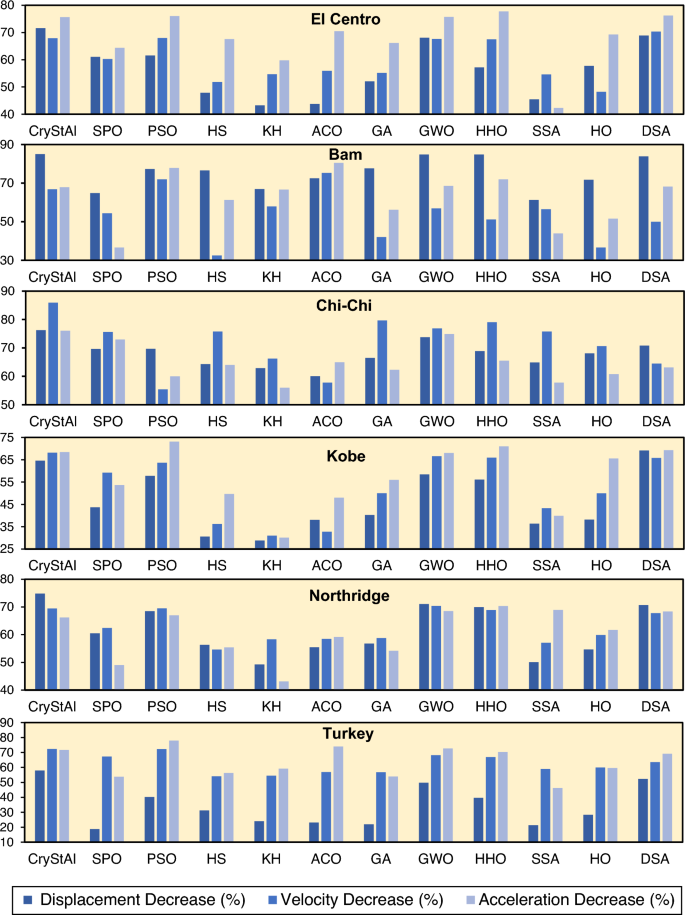
Performance of various algorithms in terms of displacement, velocity, and acceleration reductions for the 6-story structure under each earthquake scenario.

According to Figs. 8. 9, by comparing the performance of the different algorithms, it can be concluded that CryStAl consistently outperforms other algorithms in terms of reducing the displacement, velocity, and acceleration responses under all earthquakes. Despite the fact that, in some cases, other algorithms such as DSA and HHO, manage to achieve better performance in reducing responses, CryStAl achieves the highest percentage decrease in these values, indicating its effectiveness in optimizing the FOPID controller.

For the 3-story structure, Crystal reduces the displacement, velocity, and acceleration responses by 65.49, 64.90, and 63.70%, respectively, which is higher compared to the average reduction of the other algorithms by 59.23, 57.28, and 58.35%, respectively. This means that CryStAl is more successful in reducing acceleration. Moreover, in the 3-story example, HHO, SPO, GWO, and DSA turn out to be reliable algorithms, leading to considerable improvements in structural responses. For the 6-story structure, CryStAl provides exceptional reductions of 71.71% for displacement, 71.77% for velocity, and 70.98% for acceleration. Notably, these gains significantly exceed the average performance of other algorithms, which are 55.75, 59.79, and 62.34%, respectively, for the same measures.

Table 9 summarizes the control force of a FOPID controller, optimized by various algorithms for different earthquakes. The table provides the RMS values and the absolute maximum values of the control force during each earthquake for the two structures. According to Table 9, in the 3-story structure, SSA exhibited lower RMS force than other algorithms in two out of six earthquakes, ACO showed lower RMS force in three earthquakes, and DSA had the lowest RMS force in one case, i.e., under the Chi-Chi earthquake. Despite having lower RMS force values, the SSA, ACO, and DSA algorithms still demonstrated satisfactory performance. Notably, some algorithms, such as CryStAl, achieved a higher reduction in RMS force, but they also applied a higher control force. In the 6-story structure, the SSA algorithm recorded the lowest force; however, the results obtained from this lower force were not desirable in terms of other metrics.

In general, a relatively high force could lead to undesirable consequences, such as structural damage or excessive vibration. Therefore, it is essential to carefully weigh the benefits and drawbacks of these algorithms before selecting them for a specific application. On the other hand, upon closer examination, it becomes evident that lower forces come at a cost. Overall, the findings of this analysis emphasize the importance of thoroughly evaluating and selecting the appropriate algorithm for each specific structure and seismic scenario.

Statistical analysis of structural response reduction

This section investigates the effectiveness of various structural analysis algorithms in mitigating vibrations in the two building models using a non-parametric statistical test, namely, the Friedman test. The primary objective is to identify statistically significant differences in their ability to reduce displacement, velocity, and acceleration responses compared to the baseline algorithm CryStAl. The analysis reveals that CryStAl generally outperforms other algorithms across both building models and response metrics. For displacement, while CryStAl exhibits higher values than some algorithms like SPO, HS, and KH, it consistently shows notable reductions in velocity and acceleration compared to most, including SPO, PSO, KH, HHO, and SSA. These differences are deemed statistically significant, indicating CryStAl’s overall effectiveness in vibration control. However, it is important to note that statistical significance is not the only criterion; evaluating the magnitude of the difference between algorithms is also important.

Table 10 presents the results of the Friedman test across three response metrics (i.e., displacement, velocity, and acceleration) for both 3-story and 6-story building models. It reveals statistically significant differences (p-value < 0.05) in all cases, indicating that at least one algorithm (i.e., CryStAl) performs distinctly in reducing vibrations compared to others.

Finally, this statistical analysis provides valuable insights into the effectiveness of different algorithms for vibration suppression. While CryStAl emerges as a promising candidate, careful consideration of its limitations is crucial for drawing definitive conclusions and translating these findings into practical applications.