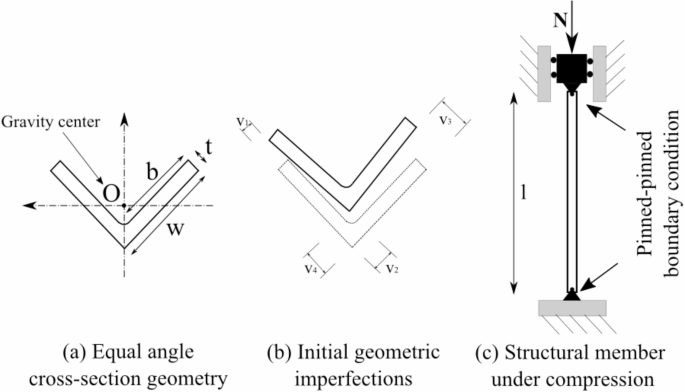
Prediction of buckling damage of steel equal angle structural members using hybrid machine learning techniques
Wang, W., Kodur, V., Yang, X. & Li, G. Experimental study on local buckling of axially compressed steel stub columns at elevated temperatures. Thin-Walled Struct. 82, 33–45 (2014).
Google Scholar
Giamundo, V., Lignola, G. P., Prota, A. & Manfredi, G. Analytical evaluation of FRP wrapping effectiveness in restraining reinforcement bar buckling. J. Struct. Eng. 140, (2014).
Megahed, K., Mahmoud, N. S. & Abd-Rabou, S. E. M. Application of machine learning models in the capacity prediction of RCFST columns. Sci. Rep. 13, 20878 (2023).
Google Scholar
Wu, F., Tang, F., Lu, R. & Cheng, M. Predicting compressive strength of RCFST columns under different loading scenarios using machine learning optimization. Sci. Rep. 13, 16571 (2023).
Google Scholar
Kollar, L. Structural Stability in Engineering Practice CRC. (1999).
Beer, F. P. & Johnston, E. R. Mechanics of Materials McGraw-Hill. (1992).
Kim, D. K. et al. Strength and residual stress evaluation of stub columns fabricated from 800 MPa high-strength steel. J. Constr. Steel Res. 102, 111–120 (2014).
Google Scholar
Shi, G., Zhou, W. J., Bai, Y. & Lin, C. C. Local buckling of 460 MPa high strength steel welded section stub columns under axial compression. J. Constr. Steel Res. 100, 60–70 (2014).
Google Scholar
Liu, Y. & Liang, Y. Satin Bowerbird optimizer-neural network for approximating the capacity of CFST columns under compression. Sci. Rep. 14, 8342 (2024).
Google Scholar
Saetiew, W. & Chucheepsakul, S. Post-buckling of linearly tapered column made of nonlinear elastic materials obeying the generalized Ludwick constitutive law. Int. J. Mech. Sci. 65, 83–96 (2012).
Google Scholar
Crisfield, M. A. A faster modified newton-raphson iteration. Comput. Methods Appl. Mech. Eng. 20, 267–278 (1979).
Google Scholar
Chang, T. Y. & Sawamiphakdi, K. Large deflection and post-buckling analysis of shell structures. Comput. Methods Appl. Mech. Eng. 32, 311–326 (1982).
Google Scholar
Stoykov, S. Buckling analysis of geometrically nonlinear curved beams. J. Comput. Appl. Math. 340, 653–663 (2018).
Google Scholar
Baydoun, I., Savin, É., Cottereau, R., Clouteau, D. & Guilleminot, J. Kinetic modeling of multiple scattering of elastic waves in heterogeneous anisotropic media. Wave Motion. 51, 1325–1348 (2014).
Google Scholar
Jiang, D., Bechle, N. J., Landis, C. M. & Kyriakides, S. Buckling and recovery of NiTi tubes under axial compression. Int. J. Solids Struct. 80, 52–63 (2016).
Google Scholar
Valeš, J. & Kala, Z. Mesh convergence study of solid FE model for buckling analysis. AIP Conf. Proc. 150005. (1978).
Stoffel, M., Bamer, F. & Markert, B. Artificial neural networks and intelligent finite elements in non-linear structural mechanics. Thin-Walled Struct. 131, 102–106 (2018).
Google Scholar
Nguyen, P., Doškář, M., Pakravan, A. & Krysl, P. Modification of the quadratic 10-node tetrahedron for thin structures and stiff materials under large-strain hyperelastic deformation. Int. J. Numer. Methods Eng. 114, 619–636 (2018).
Google Scholar
Peña, J. M., LaTorre, A. & Jérusalem, A. SoftFEM: the Soft Finite element Method. Int. J. Numer. Methods Eng. 118, 606–630 (2019).
Google Scholar
Karalis, D. G. Increasing the efficiency of computational welding mechanics by combining solid and shell elements. Mater. Today Commun. 22, 100836 (2020).
Google Scholar
Sebaaly, H., Varma, S. & Maina, J. W. Optimizing asphalt mix design process using artificial neural network and genetic algorithm. Constr. Build. Mater. 168, 660–670 (2018).
Google Scholar
Ye, F. et al. Artificial neural network based optimization for hydrogen purification performance of pressure swing adsorption. Int. J. Hydrog. Energy. 44, 5334–5344 (2019).
Google Scholar
Sadowski, Ł., Piechówka-Mielnik, M., Widziszowski, T., Gardynik, A. & Mackiewicz, S. Hybrid ultrasonic-neural prediction of the compressive strength of environmentally friendly concrete screeds with high volume of waste quartz mineral dust. J. Clean. Prod. 212, 727–740 (2019).
Google Scholar
Asteris, P. G. & Kolovos, K. G. Self-compacting concrete strength prediction using surrogate models. Neural Comput. Appl. 31, 409–424 (2019).
Google Scholar
Tran, V. L., Thai, D. K. & Kim, S. E. Application of ANN in predicting ACC of SCFST column. Compos. Struct. 228, 111332 (2019).
Google Scholar
Fahmy, A. S. & El-Madawy, M. E. T. Atef Gobran, Y. using artificial neural networks in the design of orthotropic bridge decks. Alex. Eng. J. 55, 3195–3203 (2016).
Google Scholar
Le, B. A., Yvonnet, J. & He, Q. C. Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Methods Eng. 104, 1061–1084 (2015).
Google Scholar
Kaveh, A., Eskandari, A. & Movasat, M. Buckling resistance prediction of high-strength steel columns using Metaheuristic-trained Artificial neural networks. Structures 56, 104853 (2023).
Google Scholar
Mojtabaei, S. M., Becque, J., Hajirasouliha, I. & Khandan, R. Predicting the buckling behaviour of thin-walled structural elements using machine learning methods. Thin-Walled Struct. 184, 110518 (2023).
Google Scholar
Hou, Z., Hu, S. & Wang, W. Interpretable machine learning models for predicting probabilistic axial buckling strength of steel circular hollow section members considering discreteness of geometries and material. Adv. Struct. Eng. (2024).
Ban, H. Y., Shi, G., Shi, Y. J. & Wang, Y. Q. Column buckling tests of 420 mpa high strength steel single equal angles. Int. J. Str. Stab. Dyn. 13, 1250069 (2013).
Google Scholar
Ma, T. Y., Liu, X., Hu, Y. F., Chung, K. F. & Li, G. Q. Structural behaviour of slender columns of high strength S690 steel welded H-sections under compression. Eng. Struct. 157, 75–85 (2018).
Google Scholar
Huiyong, B. & Gang, S. Wang Yuanqing. Residual stress tests of high-strength steel equal angles. J. Struct. Eng. 138, 1446–1454 (2012).
Google Scholar
Narayanakumar, S. & Raja, K. A BP Artificial neural network model for Earthquake Magnitude Prediction in Himalayas, India. Circuits Syst. 7, 3456–3468 (2016).
Google Scholar
Zweiri, Y. H., Whidborne, J. F. & Sceviratne, L. D. A three-term Backpropagation Algorithm. Neurocomputing 50, 305–318 (2002).
Google Scholar
Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
Google Scholar
Shi, Y. & Eberhart, R. A modified particle swarm optimizer. in IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360) 69–73. (1998).
Chai, T. & Draxler, R. R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 7, 1247–1250 (2014).
Google Scholar
Willmott, C. J. & Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 30, 79–82 (2005).
Google Scholar
Sarir, P., Chen, J., Asteris, P. G., Armaghani, D. J. & Tahir, M. M. Developing GEP tree-based, neuro-swarm, and whale optimization models for evaluation of bearing capacity of concrete-filled steel tube columns. Eng. Comput. (2019).
Google Scholar
Sheela, K. G. & Deepa, S. N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. (2013).
Google Scholar
Ren, Q., Li, M., Zhang, M., Shen, Y. & Si, W. Prediction of Ultimate Axial Capacity of Square Concrete-Filled Steel Tubular Short Columns using a Hybrid Intelligent Algorithm. Appl. Sci. 9, 2802 (2019).
Google Scholar
Gordan, B., Jahed Armaghani, D., Hajihassani, M. & Monjezi, M. Prediction of seismic slope stability through combination of particle swarm optimization and neural network. Eng. Comput. 32, 85–97 (2016).
Google Scholar
Kuri-Morales, A. Closed determination of the number of neurons in the hidden layer of a multi-layered perceptron network. Soft Comput. 21, 597–609 (2017).
Google Scholar
Abambres, M., Rajana, K., Tsavdaridis, K. D. & Ribeiro, T. P. Neural network-based formula for the buckling load prediction of I-Section Cellular Steel beams. Computers 8, 2 (2019).
Google Scholar
Javed, H. et al. On the efficacy of ensemble of Constraint Handling techniques in Self-Adaptive Differential Evolution. Mathematics 7, 635 (2019).
Google Scholar
Piotrowski, A. P. Review of Differential Evolution population size. Swarm Evol. Comput. 32, 1–24 (2017).
Google Scholar
Chen, T., Tang, K., Chen, G. & Yao, X. A Large Population Size Can Be Unhelpful in Evolutionary Algorithms. arXiv (2012).
Momeni, E., Jahed Armaghani, D., Hajihassani, M. & Mohd Amin, M. F. Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Measurement 60, 50–63 (2015).
Google Scholar
Zhao, Q. & Hastie, T. Causal interpretations of Black-Box models. J. Bus. Econ. Stat., 1–10 (2019).
Google Scholar
Qi, C. et al. Towards Intelligent Mining for Backfill: a genetic programming-based method for strength forecasting of cemented paste backfill. Miner. Eng. 133, 69–79 (2019).
Google Scholar
Goldstein, A., Kapelner, A., Bleich, J. & Pitkin, E. Peeking inside the black box: visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 24, 44–65 (2015).
Google Scholar
Nguyen, V. H. et al. Optimization of milling conditions for AISI 4140 steel using an integrated machine learning-multi objective optimization-multi criteria decision making framework. Measurement 242, 115837 (2025).
Google Scholar
Sun, Y., Zhang, L., Yao, M. & Zhang, J. Neural network models and shapley additive explanations for a beam-ring structure. Chaos Solitons Fractals. 185, 115114 (2024).
Google Scholar
link