Multi objective elk herd optimization for efficient structural design

Hypervolume (HV)

“Let \(\left^\left\)= \({(P*\right_^{r},\dots ,\text{a})}^{T}\), be a inferior point dominated by all the Pareto optimal objective vectors. The HV of P is defined as the volume of the objective space dominated by solutions in P and bounded by \({a}^{r}\).

where V indicates the Lebesgue measure. Hyper Volume assesses the section of the objective space occupied by the non-dominated solution set; higher values indicate better performance”⁶².

Boxplots provide useful information about the mean and distribution of hypervolume (HV) obtained for each algorithm over several runs, making them a powerful tool for visual algorithm analysis and optimization. Each box shows the median HV value, and the line inside the box represents the interquartile range (IQR) around the middle 50% of the data. The colour of the result depends on the combination of HV input, allowing a direct comparison between algorithms. Therefore, these boxes summarize the distribution and centre of the HV values ​​and provide a useful distribution pattern that shows the performance of each algorithm. Box plot analysis shows the distribution and structure of HV and shows the reliability and consistency of each algorithm. The boxplot components, including mean HV, difference and output, show the algorithm that produces the best HV. A high HV value indicates that the algorithm can capture many target regions, while a small IQR and a small group interval indicate that the algorithm is reliable and stable. The relationship between compatibility and diversity is important for effective organizational design, and managing trade-offs between competing goals is important.

Figure 19 shows the HV parameters of NSGA-II, MOEA/D, MOMPA, MOSAO, MOGNDO, and MOEHO for a typical truss problem. This shows the ability and strength of MOEHO to produce high quality pareto fronts. Compared to, algorithms such as NSGA-II and MOGNDO, MOEHO show significant improvement over HV, especially for complex problems where computational efficiency and quality of solutions are important. The comparison in these boxes shows that MOEHO is better than other algorithms, achieving the highest average HV and the lowest IQR. The small density in the centre of the boxplots of MOEHO ensures that it can pass through the selected area, find a good solution, and do this without excessive monitoring. In general, MOEHO exhibits better performance in system optimization, especially for complex multi-objective problems that require robust, diverse, and well-organized solutions.

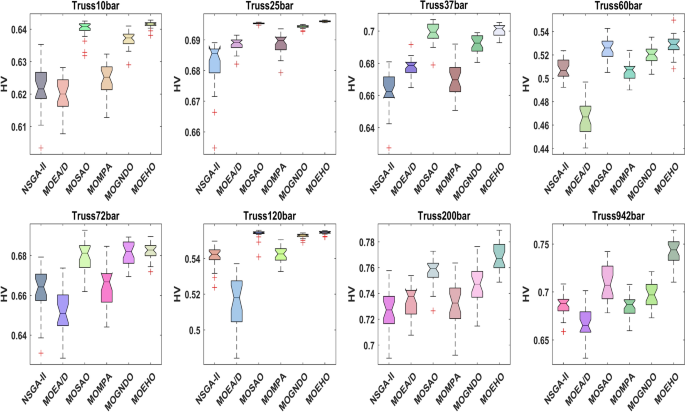
Box plot of hyper volume by considered algorithms for different truss structures.

Figure 20 illustrates the hypervolume HV trends observed across eight benchmark constraint-based design problems by comparison of accomplishment of MOEHO with several multi-objective evolutionary algorithms (MOEAs), including NSGA-II, MOSAO, and MOGNDO. These results imply that MOEHO is performing better, with faster convergence and higher final HV values than in previous studies, across all benchmark problems.

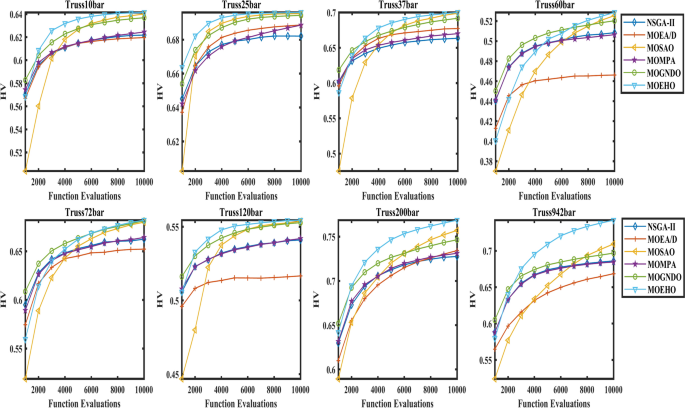
Convergence plot of hyper volume by considered algorithms for different truss structures.

The MOEHO convergence curve reveals that it is possible to rapidly find early high-quality solutions, as well as accurately estimate the Pareto-optimal front in the early stages of the optimization process. This early ‘lead’ in performance is ahead of the other algorithms, thus confirming the superiority of MOEHO in quality and diversity of the solution obtained. The MOEHO algorithm’s structure enables it to cover a large portion of the solution space while offering a good balance of two or more conflicting objectives with great precision. Exploration of objective space over the course of iterations is, thus, vital for multiobjective optimization. Given complicated solution spaces, the adaptive approach of MOEHO indeed proves to strengthen it to obtain optimality of a solution largely.

The above plots indicate the HV convergence of MOEHO to be more statistically higher than other algorithms. This shows support convergence with lesser iterations while providing uniform exploration of multi-dimensional objective space. In comparison with other algorithms, most of the times it tends to output variable solutions in the HV, and the MOEHO has got very nice and smooth transitions showing its ability to find the best solutions.By achieving fast convergence, excellent diversity, and the ability to adapt varied constraint environments, the MOEHO proves to be highly effective for complex multi-objective optimization problems. Its robust performance makes it particularly fit for answering challenging advanced engineering design challenges.

The Hypervolume (HV) values in Table 2 show the performance of MOEHO across different constraint classification problems, by comparison of its performance with other multi-objective optimization algorithms under the difficulty of the classification. For the simple 10-bar algorithm, MOEHO obtained a HV of 0.64142, a value higher than that reached by other algorithms, showing its first step in generating a well-distributed solution set. This trend continues with the 25-bar truss, where MOEHO achieved a HV of 0.69606, in line with its peers. As complexity rises with the 37-bar truss, MOEHO maintains its advantage, achieving an HV of 0.70015. This consistent performance signals MOEHO’s ability to cover the objective space effectively while maintaining high solution quality. For the 60-bar truss, MOEHO demonstrated robust performance with an HV of 0.52869, indicating its adaptability to handle larger structural design challenges without compromising on efficiency.

In the case of a 72-bar truss, MOEHO achieved a hypervolume (HV) value of 0.68197, maintaining its consistent performance in terms of convergence and diversity when compared to other algorithms. This trend continued with the 120-bar truss, where MOEHO recorded an HV of 0.55443, further confirming its capability to deliver high-quality solutions even as the complexity of the truss structures increased.

The accuracy and reliability of MOEHO tend to greatly improve with the increasing complexity of the optimization problem in consideration. Regarding the 200-bar truss, MOEHO recorded an impressive hypervolume (HV) value of 0.76864, proving its capability of exploring and optimizing even in quite large design space. This advantage was affirmed during the execution of the highly complex problem of the 942-bar truss, where the value of the hypervolume generated by MOEHO algorithm was HV = 0.74213, which is better than that of all other algorithms under consideration. These findings demonstrate that MOEHO can provide optimization services in an effective and dependable way even in most complex problem situations.

As shown in the Table 3, MOEHO steadily attained the highest HV across all assessed truss configurations emphasizing its superior convergence and Pareto front solutions diversity. This consistent execution illustrates its efficiency and versatility in solving problems of structural optimization. MOEHO’s ability to optimize with respect to different levels of problem difficulty, proves it as an effective algorithm for multi-objective optimization in structural engineering.

Table 3 showcases the remarkable strength of the MOEHO algorithm as the best performing algorithm for benchmark truss optimization problems considered in the research. Looking at the 10-bar truss, MOEHO records an excellent mean rank of 5.6667 which is much higher than the competing algorithms, with MOEA/D identified as the next best. The trend persists in the 25-bar truss where MOEHO also attains number one position with a score of six confirming its competent in higher order problems. For the 37-bar truss problem, MOEHO has an effective rank of 5.4444 which is still better than the performance of rival methods. When solving the 60-bar truss problem, the associated rank for MOEHO is 5.2963 demonstrating again its capability of producing best optimization results. The same trend persists in the 72-bar truss problem where MOEHO possesses a rank of 5 as well, further reinforcing its dominance in comparison to even the MOSAO approach. For 120-bar trusses that are even more intricate, MOEHO’s rank of 5.4074 indicates some upper hand over MOEA/D as it is also able perform well on more difficult optimization problems as well.

This dominance has also been observed in the problem concerning the truss of 200 bars when most of the time the algorithm obtaining the rank 2 is MOEHO and the rank of this algorithm is 5.7037. And also exhibited in the analysis of the 942-bar truss problem, the most complicated one assessed, the ranking assigned to MOEHO was the highest at 5.7778 indicating its effectiveness in solving very complicated structural designs. Five additional algorithms are compared to MOEHO: NSGA-II, MOEA/D, MOGNDO, MOMPA, and MOSAO, employing the mean ranks over eight test sets. Data collected from such a case supports the statistical rankings conferred, with p-values between 8.84E-25 and 2.60E-16, stressing the significance of the MOEHO performance. These low p-values confirm the algorithm’s.

Diversity analysis by IGD metric

“Inverted Generational Distance: Assuming P* is the set of points evenly spaced on the Pareto front, P as the solution set obtained from an EMO algorithm. The Inverted Generational Distance (IGD) of the set P is given as follows:

where dist (z; P) is the distance in Euclidean space from the point z to the closest point of the set P. To perform this calculation, however, it is necessary to sample enough points from the PF to construct P*.”

Inverted Generational Distance (IGD) is an evaluation metric that computes the distance between a given generated Pareto front and the true Pareto front by determining the average distance between the points of the given generated Pareto front and the closest points of the true Pareto front. It is better to say that lower IGD values signify better convergence, which means that generated Pareto front solutions are close to the true Pareto front. This parameter is often employed for the evaluation and implementation of multi-objective optimization techniques as it offers a quantitative measure of how close the estimated Pareto front is to the considered ideal Pareto front⁶³.

Boxplots present a simplified but effective depiction of the performance of the algorithm in a way that allows understanding both performance over time and the extent of the performance across time. With specific regard to Inverted Generational Distance (IGD), the use of boxplots provides an effective means of depicting the performance of algorithms on various ranges of truss design optimization problems. Policymakers can use comparisons involving boxplots to evaluate algorithm reproduction, performance variability and outliers, for example. Rather this analysis assists to detect those algorithms which do not only perform well but can be relied upon to give a close estimation of the True Pareto front.

In the evaluation of the boxplots, an algorithm that has a consistently less median IGD, a low value in the interquartile range (IQR), and few if any outliers for every truss design problem, will have good stability and good reliability. Such algorithms perform better when it comes to the task of moving along the Pareto front, and hence solve both trivial and sophisticated optimization problems with ease. The advantage of boxplots, in gauging how potent the algorithms are, is that they are used to record how well two performance metrics are sustained across different degrees of complexity of the design problems from the easiest to the toughest. Such a system of evaluating and comparing the efficiency of different algorithms is quite useful to engineers in determining the appropriate algorithm for a particular design work.

The boxplots represent results of the different configurations of the truss in such a manner that it includes Truss10bar, Truss25bar, Truss37bar, Truss60bar, Truss72bar, Truss120bar, Truss200bar and Truss942bar. This graphical representation analyses the performance and its deviation of the algorithms and complements other views of the Algorithm’s effectiveness including the overview of their use on truss optimization problems as shown in the Fig. 21.

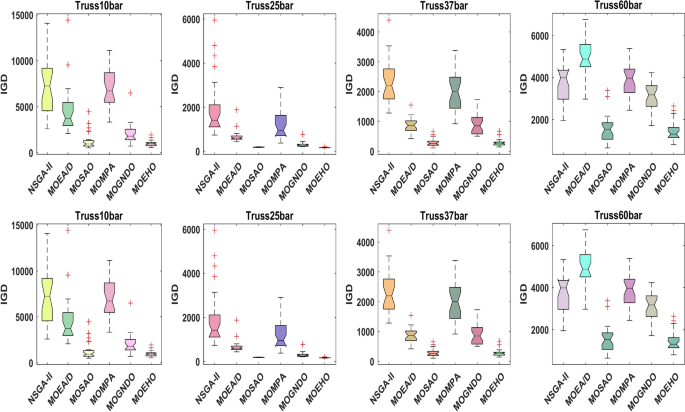
Box plot of IGD values by considered algorithms for different truss structures.

The Inverted Generational Distance (IGD) is a decisive metric for evaluating the effectiveness of solutions in approximating the True Pareto front. A lower IGD value implies a closer position of the obtained solutions to the optimal front, implying better convergence and solution quality. In the Truss10bar optimization problem, MOEHO exhibits a remarkably low median IGD, featuring its strong convergence capabilities in simpler truss structures. Its boxplot shows the lowest IQR value among the algorithms, meaning a consistent performance with least variability between iterations and problems. In contrast, MOMPA and MOSAO have wider distributions of IGD, which imply failure to converge towards the Pareto front. MOEA/D, MOGNDO, and NSGA-II have higher values of IGD and wider spreads, which suggest that they cannot reliably approximate the optimal solutions.

Furthermore, this is further enhanced with the dominance of MOEHO in solving the Truss25bar problem. It showed the smallest median IGD and IQR, therefore, ensuring the stability and its repeat ability of generating high quality solutions. The MOMPA and NSGA II could not deliver on convergence, as the boxplots that had a larger area with outliers show many inconsistencies for efficient convergence toward the Pareto front. These outliers indicate the presence of a wide range of performance variability, while for MOEHO, the tight IQR in addition to the low median IGD indicated the potency of the algorithm in handling problems at any level of complexity. For Truss37bar, MOEHO persists with its superior performances. It becomes excellent in the treatment of structural optimization problems of moderate complexities that further ascertain its ability in dealing with challenging design landscapes. The Truss60bar configuration has very low median IGD and a narrow IQR; it is quite reliable concerning the handling of more challenging optimization tasks. The increase in problem complexity by means of larger design spaces and more constraints generally results in the fact that median IGD values for all algorithms increase. This pattern is very clear in the Truss72bar problem, where MOEHO continues to stand out by having a low median IGD and minimal variability, thus demonstrating consistency in producing reliable solutions despite increased complexity.

In the Truss120bar problem, the optimization task is more persistent. Although MOEHO achieves a competitive median IGD, its IQR expands by a small amount. Again, an increase in variance across all algorithms will be noted when applying the algorithms to more difficult problems. Even with this minor increase, MOEHO remains an assured performer. In the Truss200bar configuration, MOEHO again does a good job to achieve a low median IGD, though IQR increases a little. The results confirm that MOEHO is consistent in generating solutions close to the Pareto front even in large-scale structural optimization problems. Its performance is reflected in its adaptability and reliability in dealing with high-dimensional and constrained design optimization problems.

The Truss942bar problem is the most complex benchmark of the present work. Even at its extreme complexity, MOEHO displays a relatively low median IGD, just with a limited extension of the IQR. On the contrary, the distribution of the competitive algorithms shows more elevated IGD values, spreads, and an increased number of outliers, signalling that convergence might be problematic, especially for so difficult a problem. The performance of MOEHO on this complex problem highlights its amazing sturdiness and adaptability, making it a dependable algorithm even under the most challenging optimization conditions.

Consistent results with slight variability made MOEHO a dependable option for the solving of intricate problems in truss design optimization. The performance metrics of various MOOAs integrated in NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, and MOEHO, which are compared with the performance of the eight benchmark truss structure problems as shown in Fig. 22 while the benchmark problems are composed of a simple 10-bar truss problem and the most complex 942 bar truss problem. Plot of the increase in Inverted Generational Distance (IGD) values with an increase in function evaluations. IGD values lower are better since it more approximates the True Pareto Front, hence solutions obtained are of better quality and convergence.

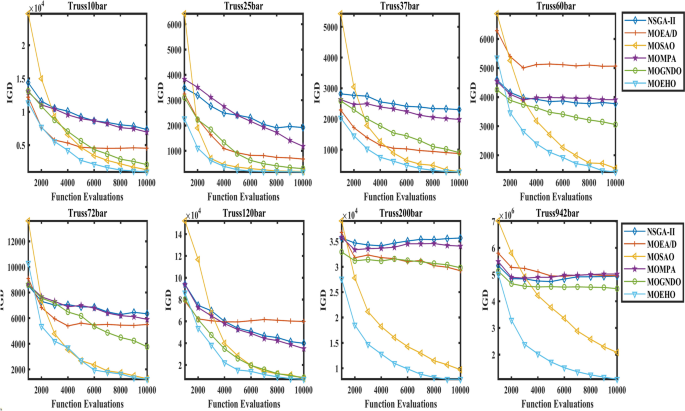
Convergence plot of IGD by considered algorithms for different truss structures.

Looking at the results, some algorithms seem to have a higher rate of convergence, that is, lower IGD values are realized with fewer function evaluations. The performances of MOEHO and MOSAO will always be at the upper range especially with respect to simple structures like the 10-bar and 25-bar trusses. They also exhibit a quick decrease in IGD and can get optimal solutions in a short time compared to others. However, this is not the case for MOMPA and NSGA II as they have a tendency of achieving lower convergence rate even with the simpler trusses. In the 200-bar and 942-bar trusses complex problems, the IGD values are still high indicating a poor approximation towards the Pareto front.

MOEHO outperforms others in all truss problems. Its IGDs remain minimum against the function evaluation over the problem complexity periphery. This behaviour reinforces the observations concerning the efficiency of MOEHO in addressing any given optimization problem. In addition, the way it achieves solutions within a short period of time with high accurateness for structural optimization problems makes this algorithm unique. On the other hand, while MOEA/D can compete well in simple designs problems. The ability of MOEHO to endure such simple and very complicated trusses designs illustrates its flexibility.

The results demonstrated in Fig. 22 illustrate more clearly the benefits of using MOEHO for multi-objective structural problems, its convergence curves show that the rate of convergence was faster and yet more stable. MOEHO produces diverse as well as the accurate approximations of the Pareto front. From these results, it may be concluded that MOEHO is an efficient and effective multi-objective truss design optimization algorithm.

Table 4 contains a comprehensive evaluation of the efficiency of MOEHO in the solution of the benchmark truss optimization problems anchored on the Inverted Generational Distance (IGD) metric. For the simple optimization problems such as the 10-bar truss, the algorithm exhibited an IGD of 9.5271e + 2. This illustrates MOEHO’s effectiveness in handling simple structural optimization problems. The algorithm is reliable and capable when dealing with simple truss structure problem–solution. The same is true for the problems that are slightly difficult, for instance, the 25-bar truss problem which had an IGD value of 1.6456 e + 2 for the MOEHO. This is a good demonstration of the method’s adaptability and robustness to handle the more challenging optimization problems and to perform well. For more complex structures within the moderate range, such as the 60-bar and 72-bar trusses, MOEHO attained IGD values of 2.7386 e + 3 and 1.4243 e + 3, respectively. It can easily be observed that the algorithm performed efficiently in solving the challenging optimization problem of approximating the Pareto optimal front.

In problems of very high complexity, MOEHO’s real strength can be observed. For the 942-bar truss structure, the algorithm has an IGD value of 1.0793 e + 6, indicating that it is capable of handling complex optimization problems. These results highlight the flexibility and robustness of MOEHO in handling different levels of problem complexity. Despite MOEHO’s inability to regularly provide the least IGD for each test, its efficiency in finding approximate solutions makes it more suitable for addressing challenging optimization tasks. The overall performance of this algorithm indicates how reliable and versatile it is. This makes MOEHO an efficient tool to solve multi-objective structural optimization problems.

Table 5 gives an extensive analysis of rank based on IGD values and comparison of p-values for MOEHO and various MOOAs over 8 different truss optimization problems. The p-values show the statistical significance of MOEHO performance, which proves its efficiency when is used in optimization problems. For example, during the solution of the 10-bar truss problem, MOEHO algorithm was ranked 1.5161 and scored a p-value of 4.16E-25 giving strong significance. This general tendency is also observed in more complicated issues such as the case of 25-bar and 37-bar truss configurations where the ranks were 1.0968 and 1.6129 respectively and p-values were 1.11E-28 and 1.63E-27. These results clearly indicate the superiority of MOEHO over its competitors in different kinds of optimization processes.

As the Tusse structures become more complex, the MOEHO keeps giving better outcomes. For instance, consider the 60-bar and 72-way trusses. The observed p values of 1.08E-24 and 8.61E-24 respectively shows a significant effective difference in favour of MOEHO. In the complex 942-bar truss problem almighty MOEHO scored a p-value of 6.81E-24 again reinforcing its effectiveness under extreme cases. The presence of this pattern of p-values, which are quite low for many problems, is further indicative of the applicability of MOEHO computational tool in multi-objective truss optimization to be carried out optimally.

Moreover, the Friedman test ranks analysis shown in Table 5 also helps to view the performance of MOEHO in quantitative terms. Scores in the Friedman test are inversely related to performance with MOEHO scoring 1.5143 in 10-bar truss problem indicating best performance on simple problems. In the case of 60-bar truss problem, MOEHO scored 1.5429 confirming it as excellent performer. Despite the intricacies of the 942-bar truss problem, MOEHO earned a 1.1714 score evidencing its efficiency in solving complex optimization problems that are very difficult to solve.

From these observations, it can be inferred that besides ease of use, MOEHO is a flexible and strong tool when it comes to optimization procedures. Given the fact that it consistently records lower IGD values in addition to strong statistical performance in numerous truss setups, MOEHO is an effective optimization algorithm for solving complex problems in multi-objective optimization. MOEHO is combined with encouraging statistical results and effectiveness in its computation making it suitable for use by design engineers and researchers to solve problems in structural optimization.

Quality assessment of non-dominated solutions by spacing matrix

“Spacing (SP) measures the evenness of spacing between adjacent solutions along the Pareto front, aiming for a balanced distribution without clustering or excessive gaps. Lower SP values indicate more uniformly spaced solutions.

where, \({N}_{0}\) denoted the number of pareto fronts and \({d}_{i}^{spacing}\) denotes the Euclidean distances between consecutive solutions in the objective space. Spacing assess the spread and distribution of solutions across the Pareto front”⁶⁴.

The box plots depicted in Fig. 23 illustrate the SP values corresponding to various optimization challenges in truss structures, as evaluated by multiple multi-objective algorithms, including NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, and MOEHO. The SP metric is an essential indicator of the uniformity of solution distribution along the Pareto front; lower SP values signify a more evenly distributed set of solutions, which is generally preferred in optimization scenarios. MOEHO stands out for its consistently superior performance across all tested truss structures, demonstrating an impressive capacity for both SP distribution and convergence.

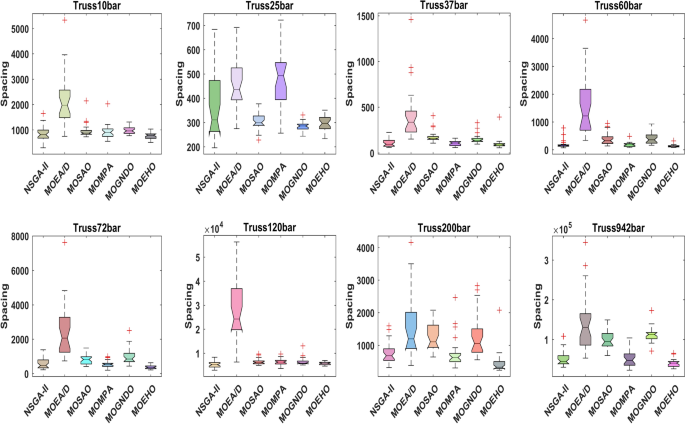
Box plot of SP values by considered algorithms for different truss structures.

The boxplots indicate that MOEHO provides more low and stable SP values in comparison to the other methods, which also support a more uniform set of solutions on the Pareto front. This ability of the algorithm is critical to accurately locate the solution point, this helps to improve quality and reliability of the algorithm. The consistency across diverse truss problems and capacity to preserve this uniformity makes MEHO applicable for complex optimization problems.

The convergence graph presented in Fig. 24 indicates that MOEHO offers higher speed and a stable solution distribution. The performance analysis of MOGNDO and NSGA-II shows that the convergence rate is slow and the solution’s reliable distribution cannot be achieved when MOGNDO and NSGA-II are used. This result indicates that they lack the capacity to create systemic (widespread) solution on complex problems.

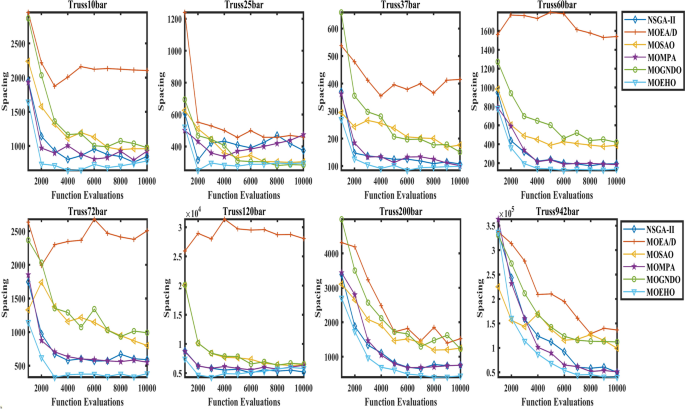
Convergence plot of SP Values by considered algorithms for different truss structures.

MOEHO’s capability to deliver lower development time, and sustainable solution plays a decisive role in truss design optimization. This capability of MOEHO to search the solution space in an efficient manner to yield diverse solutions for optimization problems of varying complexity makes it suitable for the multi-objective optimization problems of truss structures.

SP is quite important for multi-objective optimization since it measures the evenness of how the solutions are spread in the Pareto front. Very low values of SP suggest a good and desired distribution of solution set for optimum performance improvement. In optimization problems, uniform distribution is necessary because optimally it permits full representation of the Pareto front, since solutions are not overly dense in any area, but rather well and evenly spread throughout the solution space. A Comparative study of the SP values of some Algorithms: NSGA-II, MOEA/D, MOMPA, MOGNDO, MOSAO, MOEHO for several truss optimization problems shows how these algorithms could distribute the solutions satisfactorily. The SP results are presented in Table 6, where the MOEHO outperforms all other truss design problems considered.

As an example, in the 200-bar truss problem, the MOEHO algorithm yields a SP value of 4.3566e + 2, while for the second-best method, MOMPA is equal to 7.7962e + 2. Since the SP value is considerably low for MOEHO, it can be presumed that the solutions proposed by MOEHO are more diversified and extended along the curve of the Pareto front, even in the more complicated and higher-dimensional optimization problems. It can therefore be inferred that the MOEHO executes its task extremely well. The MOEHO produces the solutions which are widely scattered even in the challenging situation, which is a major requirement to guarantee full optimization.

The difference in SP values between MOEHO and the rest of the algorithms confirms that the other algorithms generate more clustered solutions, which are indicated by higher SP values. Such clustering tendencies would hinder the comprehensive nature of optimization algorithm. A statistical evaluation of p-values shows the effectiveness of MOEHO in comparison with other state of the art constrained multi objective optimization techniques used on eight different truss designs. Analysis of the statistics produced p-values between 1.30E-24 and 6.14E-15 implying that the observed differences in the relative SP performance are very large.

Such statistical evidence strengthens the assertion that MOEHO is better than competing algorithms at generating solutions which are evenly spaced on the Pareto front. Such a benefit also demonstrates the potential of MOEHO in solving complex multi-objective optimization problems, particularly in design processes where the solutions must be evenly spread out and the entire solution space must be utilized. This spanning superiority is consistent with how spaced this algorithm is, proving its strength and the optimum and dependable solutions it can render within many optimization problems.

Table 7 displays the outcomes of the Friedman rank test, showcasing MOEHO’s impressive performance with consistently lower average ranks across various truss design challenges using the SP metric. These lower average ranks signify MOEHO’s superiority in maintaining a diverse and well-distributed range of solutions, crucial for efficient multi-objective optimization in intricate engineering scenarios.

The favourable ranks achieved by MOEHO affirm its capacity to generate a broad spectrum of solutions that are appropriately distributed along the Pareto front the notable difference in ranks, supported by high P-values, underscores MOEHO’s dominance over its competitors concerning solution SP. This exceptional performance underscores MOEHO’s effectiveness in handling solution diversity, a vital aspect for the reliability and adaptability required in tackling intricate structural engineering design and optimization issues. The capability to produce a varied set of solutions not only enriches decision-making quality but also ensures a thorough exploration of the solution space.

The computational runtime for different truss structures across various algorithms reveals significant variations, particularly for complex structures with a higher number of elements. While NSGA-II demonstrates the highest runtime in most cases, MOEHO and MOGNDO exhibit relatively lower computational costs for larger structures, indicating their efficiency in handling increased complexity as shown in the Table 8.

In MO optimization, it is generally a compromise between efficiency and solution quality. Although Table 8 indicates that MOEHO is not always the quickest algorithm, its slightly longer runtime is worthwhile for its better convergence performance, evident in the HV, IGD, and SP metrics. The extra computational expense comes from MOEHO’s adaptive strategies, such as dynamic parameter adjustment and an information feedback approach, that promote exploration and keep a diversified Pareto front. Compared to algorithms such as MOSAO and MOGNDO, they might gain quicker runtimes but may lose in solution diversity and convergence quality. To demonstrate this balance, a comparative study of runtime and performance measures is given, showing that MOEHO provides a better trade-off and, thus, is a competitive option for structural optimization with a moderate rise in computational time.

According to Table 8 the runtime analysis shows MOEHO does not achieve the fastest results for all truss structures. The balance between solution quality and runtime serves as an essential reason to accept MOEHO’s elevated computational costs in particular situations. The runtime performance of MOEHO shows slightly longer durations than MOSAO or MOGNDO for basic structures such as 10-bar and 25-bar trusses but proves its superiority through better solution quality and diversity when dealing with complex optimization problems. MOEHO shows competitive runtime performance across various complex structures such as the 200-bar and 942-bar trusses but produces superior solutions as confirmed through superior Hypervolume (HV) and Inverted Generational Distance (IGD) and Spacing (SP) metrics observations. MOEHO achieves an optimal balance between efficient computing and excellent solution quality which proves beneficial for cases requiring precise robust solutions that adequately explore diverse Pareto fronts.

The ability of MOEHO to maintain proper exploration–exploitation balance in engineering design applications prevents it from converging prematurely towards suboptimal solutions while ensuring solution accuracy and reliability. The success of traditional algorithms to produce diverse accurate Pareto front approximations becomes crucial in high-dimensional optimization problems with constraints. MOEHO’s slightly elevated computational requirements become worthwhile since it produces solutions that both match the true Pareto front more precisely and distribute solutions uniformly which helps decision-makers make confident optimal design selections. MOEHO demonstrates robust performance through adaptive parameter controls together with dynamic strategy-based selection features which enhances its ability to resolve complex engineering problems better than most other algorithms.

The analysis of essential trends in the figure captions delivers a thorough performance review of MOEHO when optimizing truss structures. The 10-bar truss problem in Fig. 11 demonstrates that MOEHO produces superior Pareto fronts than NSGA-II, MOEA/D, MOMPA, MOGNDO and MOSAO while maintaining excellent convergence and diversity. This algorithm produces a well-organized set of solutions that closely follows the true Pareto front because it demonstrates robustness when dealing with small-scale structural optimization problems. MOEHO generates a denser Pareto front for the 25-bar truss problem which spans across a wider area in the objective space as illustrated in Fig. 12. The algorithm proves its capability to solve medium-scale optimization problems while maintaining diverse solutions.

In the 37-bar truss problem of Fig. 13 MOEHO demonstrates a Pareto front with excellent distribution and minimal clustering because it effectively balances exploration and exploitation. The algorithm enhances promising solutions while preserving diversity which makes it suitable for moderately complex structural optimization problems. The MOEHO algorithm demonstrates scalability through its Pareto front generation for the 60-bar truss problem as shown in Fig. 14. The optimization process demonstrates effective handling of complex problems because solutions are distributed evenly while gaps and clusters remain minimal. The MOEHO algorithm demonstrates a uniform distribution of solutions in the Pareto front for the 72-bar truss optimization problem as shown in Fig. 15. The optimization algorithm demonstrates excellent search space exploration capabilities with precise results which makes it suitable for high-dimensional problems.

MOEHO demonstrates its capability to produce a properly distributed Pareto front for the 120-bar truss problem through minimal computational requirements as shown in Fig. 16. The algorithm manages exploration against exploitation activities to yield high-quality and diverse solutions. MOEHO demonstrates efficient performance in large-scale optimization problems through Fig. 17 by maintaining convergence and diversity in the Pareto front when solving the 200-bar truss. The results in Fig. 18 display how MOEHO outperforms competing algorithms with its exceptional ability to optimize the highly complex 942-bar truss system alike its superiority in solution quality alongside computational efficiency. MOEHO generates a Pareto front that spans a wide area of the objective space thus demonstrating its ability to address complex high-dimensional multi-objective optimization problems effectively.

The superiority of MOEHO in truss structure optimization problems becomes evident through Fig. 19 which shows box plots of Hypervolume (HV) values. The superior HV values obtained by MOEHO demonstrate its capability to effectively explore the objective space and create high-quality solutions. The small interquartile range (IQR) confirms both the stability and reliability of the results. Figure 20 illustrates how MOEHO achieves higher Hypervolume values during fewer function evaluations compared to alternative algorithms. The algorithm demonstrates quick discovery of promising search areas during its early optimization period because of its efficient space exploration capabilities.

The assessment of Inverted Generational Distance (IGD) as a Pareto front approximation quality metric occurs in Figs. 21 and 22. The box plots in Fig. 21 show MOEHO produces consistently lower IGD values which proves its superior ability to approximate the true Pareto front with diversity maintained. Figure 22 demonstrates that MOEHO efficiently reaches low IGD values through minimal function evaluations thus proving its ability to solve complex multi-objective problems effectively.

The spacing (SP) values presented in Figs. 23 and 24 demonstrate that MOEHO effectively produces solutions with uniform distribution. Figure 23 demonstrates MOEHO produces lower SP values throughout all trials which indicates its strong capability for maintaining solution diversity. Figure 24 shows that MOEHO finds diverse well-spaced solutions using fewer function evaluations thus demonstrating its efficiency in simultaneously reaching convergence and diversity.

The interpretations detail MOEHO performance trends through evaluations which demonstrate its solid convergence and diverse results and computational efficiency on different structural optimization problems. The algorithm shows potential for extending its application to various multi-objective optimization challenges which surpasses structural engineering fields.

The MOEHO algorithm proved to be successful in solving structural optimization problems of various complexity. It performs best in comparison with other algorithms since it has quality outputs, which are processed faster. The above performance in handling problems of varying complexity shows that MOEHO has practical applications where speed and good-quality results are needed. However, on larger truss structures such as the Truss72bar configuration, MOEHO suffers somewhat in terms of computational speed, but its quality of solution increases with the size of the problem. This balancing of computational speed and solution quality is important for the field of structural optimization where results need to be efficient as well as effective. Although MOEHO has been shown to have excellent performance in structural optimization, its extension to other fields is an open area for investigation. One of the limitations is its computational expense on large-scale problems, which, while compensated by better solution quality, can be further improved with parallel computing or surrogate-assisted modeling. Another area that has not yet been thoroughly investigated is the performance of MOEHO in fields like energy systems, aerodynamics, and robotics. Subsequent studies may entail modifying MOEHO for real-time and dynamic optimization problems and incorporating machine learning-based approaches to improve convergence rates and computational effectiveness, extending its applicability to a wide range of engineering disciplines.

The fact that MOEHO maintains a proper distribution of solutions even when the computational requirements increase reinforces its status as an effective and reliable choice for more complex multi-objective optimization problems. The consistency of MOEHO’s performance with problem sizes underlines its adaptability and robustness, making it a very useful tool for engineers who are dealing with complex structural design tasks. Thus, MOEHO is not only superior in providing solutions but also shows resistance in the face of increasing computational challenges.

MOEHO achieves fastest convergence speed against other algorithms during the optimization of benchmark truss structures. The hypervolume (HV) and inverted generational distance (IGD) metrics show that MOEHO achieves better high-quality solutions more quickly than NSGA-II, MOEA/D, MOMPA, MOGNDO, and MOSAO algorithms. MOEHO demonstrates enhanced early-stage optimization efficiency through its achievement of an HV value of 0.6414 in the 10-bar truss problem before other algorithms reach similar results. The rapid convergence rate of MOEHO continues throughout the optimization process of the 942-bar truss despite its complex structural nature.

The Pareto front diversity of MOEHO is demonstrated through its excellent performance in the spacing (SP) metric. The algorithm generates solutions with equal distribution which leads to complete coverage of the Pareto-optimal set. MOEHO demonstrates superior solution distribution in the 200-bar truss problem through its SP value of 4.4252e + 2 which surpasses alternative algorithms. A diverse set of solutions stands essential for engineering design because it supports better decision-making by providing various trade-offs between competing project objectives. The performance of MOEHO maintains its strength when the truss structures become progressively more complex. In solving the 10-bar truss problem MOEHO achieves superior performance with an HV of 0.6414 and an IGD of 9.6527e + 2 compared to other tested algorithms. The 942-bar truss structure presents no challenge to MOEHO which generates high-quality results with HV at 0.7421 and IGD at 1.0793e + 6. MOEHO displays its ability to expand into high-dimensional problems because of its flexible architecture that maintains operational reliability when handling multi-objective challenges.

The Friedman rank test establishes MOEHO as superior by showing consistently low average ranks in every test scenario. In the 25-bar truss problem MOEHO obtains a ranking position of 6 which demonstrates superior performance compared to other algorithms. The statistical significance of MOEHO’s performance becomes evident through its low p-values which reach 8.84E-25 in the 25-bar truss problem.

The study improves reproducibility by completely explaining MOEHO’s mathematical model which includes Pareto-Dominance Ranking and Crowding Distance Approach and Elite Retention and Adaptive Parameter Settings. The implementation approach includes both pseudo-code and flowcharts to help developers. Future researchers can replicate the findings because this research provides complete information about all algorithm-specific parameters and population size and maximum iterations. The study provides comprehensive descriptions of benchmark problems which include multiple truss structures from 10-bar to 942-bar that specify design variables together with constraints and loading requirements. The study defines HV, IGD, and SP formally to ensure consistent evaluation practices. The conclusions benefit from statistical robustness because the study employs the Friedman rank test together with p-values for validation.

The paper advances previous research through its addition of flowcharts and visual aids which demonstrate the operations of EHO and MOEHO. The optimization results become more understandable through visual representations of Pareto fronts that accompany each truss problem. The mathematical descriptions of MOEHO components including the rutting season and calving season and selection mechanisms appear in a clear fashion to guarantee methodological transparency. The research improves understandability through assessments utilizing boxplots and convergence plots as they display MOEHO’s efficiency through visual charts. The study defines technical terms alongside multi-objective optimization concepts in a way that makes the information understandable for both experts and non-experts in the field.